Physics 208 - Lab 2 - Ray Optics
Introduction
Equipment check
Please make sure your station has all of the following items. If not, check again, then talk to your lab instructor.

- 1 Incandescent source box w/ power supply.
- 2 Converging lenses
- 1 Screen
- 1 Index Card
- 1 12" Ruler
Warm up Exercises
Make some images
Set up a lamp, a converging lens, and the screen on the optical track, as shown. Plug the lamp in and arrange the screen and the lens so that you obtain an image of the source on the screen. (You should face the lamp so that the arrow and the cross cutout is projected towards the screen.)
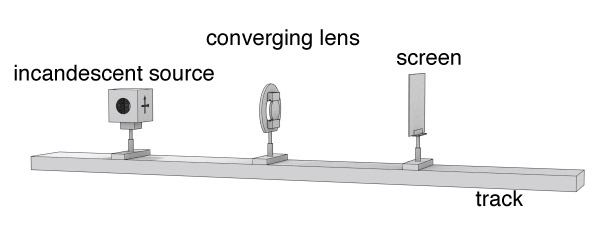
Find a location that creates an inverted, real image of the source shape on the screen. Make sure the image is focused as much as possible, and that its height matches the source height as much as possible. What are your object and image distances?
Now arrange the lens and the screen so that there is a real inverted image, but with a magnification of 1.5. What are the object and image distances? Do they make sense?
Block a Lens
What would happen to the image on the screen if you took an index card and blocked just the upper half of the lens with it, as shown in the drawing?
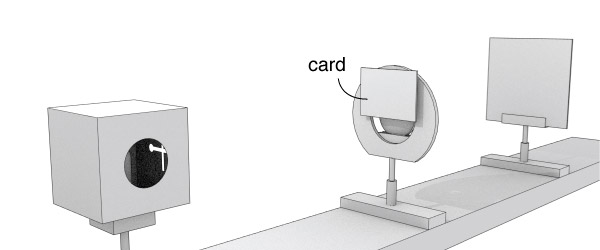
Now try it with the actual index card. Did your prediction come true?
Experiment 1: Determine $n$
The goal of this experiment will be to figure out, experimentally, if the material of the two converging lenses is the same. (i.e. do they have the same index of refraction.)
Some relations that might be useful:
- The lensmaker's equation: $$ \frac{1}{f}= (n-1)\left( \frac{1}{R_1}-\frac{1}{R_2} \right) $$ where $f$ is the focal length, $n$ is the index of refraction, and $R_1$ and $R_2$ are the radii of curvature of the front and back surfaces. In this case, you can assume the lenses are both symmetric so $R_1$ = $R_2$.
- The thin lens equation: $$\frac{1}{p} + \frac{1}{i} = \frac{1}{f}$$ where $p$ is the object distance, $i$ is the image distance, and $f$ is the focal length.
- One lens has a radius of curvature of 20.7 cm, the other is 10.3 cm.
After performing your experiment, put your two values in these boxes:
Do you think the two materials are the same?
Report Questions
1. Your report should include a description of the experiment you devised to determine the two indices of refraction. You should discuss how confident you are in the measurement, and what basis you have for saying they are the same or different.
2. Find a table of n values on the internet and see if you can determine the exact type of material.
3. Make sure to include a ray diagram showing how you produced the images.
Experiment 2: Build a telescope
You should have the two converging lenses from the first part. One has a 10 cm focal lens (it's thicker), the other has a 20 cm focal length. Set up the incandescent source and the 20 cm lens on the track, with the lens at roughly the midpoint. Put the screen in place until an image forms on it. Is this a real or virtual image?
Now, you'll want to use the second lens, the 10 cm lens, as an eyepiece to magnify the image from the first lens. Put the second lens past after the screen, and move it until you can look through the second lens and see the screen in focus. Now remove the screen, and the light source. You should have a telescope if you look through the objective lens straight ahead.
Try to set up the telescope as it is on the track so that you can see something in the distance. Perhaps a drawing on the chalkboard, or a poster on the far wall. (Yes, it's not a very mobile telescope, but try to be creative.) Take a picture with your phone looking through the two lenses, and then another picture of the distant object from the position, without the lenses. Compare the apparent size of the object.
Here's an example of what you should see. The globe (the distant object) is noticeable bigger when looking through the telescope! As it should be.

Report Questions
1. Calculate the magnification of your telescope.
2. Draw a ray diagram of the telescope.
3. Record images like the globe image above to check the magnification values that you obtain analytically.
